SOLUTION: find the radius of the circle inscribed in the triangle bounded by the lines x-y+4=0, 7x-y-2=0 and x+y+4=0. actually i graph the equation and prove that x-y+4 is perpendicular

Algebra ->  Equations -> SOLUTION: find the radius of the circle inscribed in the triangle bounded by the lines x-y+4=0, 7x-y-2=0 and x+y+4=0. actually i graph the equation and prove that x-y+4 is perpendicular      Log On


   

Question 86741: find the radius of the circle inscribed in the triangle bounded by the lines x-y+4=0, 7x-y-2=0 and x+y+4=0.
actually i graph the equation and prove that x-y+4 is perpendicular to the line x+y+4. got all the points of the triangle (1,5), (-4,0) and (-1/4, -3.75), got stuck with the circle thing.. could you help me please?
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
find the radius of the circle inscribed in the triangle bounded by the lines x-y+4=0, 7x-y-2=0 and x+y+4=0.
actually i graph the equation and prove that x-y+4 is perpendicular to the line x+y+4. got all the points of the triangle (1,5), (-4,0) and (-1/4, -3.75), got stuck with the circle thing.. could you help me please?
That's not quite the way to do the problem:

The formula is
                                           TRIANGLE'S AREA
RADIUS OF INSCRIBED CIRCLE OF TRIANGLE = --------------------
                                          HALF ITS PERIMETER

We first find the three corners of the triangle:

 x - y + 4 = 0
7x - y - 2 = 0

Solve that pair and get one corner point (1,5) 

 x - y + 4 = 0
 x + y + 4 = 0

Solve that pair and get the second corner point (-4,0)

7x - y - 2 = 0
 x + y + 4 = 0

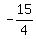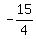Solve that pair and get the second corner point (-1%2F4,-15%2F4)

Now we find its area, using the determinant formula:


`                         |x1 y1 1|
A = absolute value of:  1%2F2|x2 y2 1|
`                         |x3 y3 1|


`                         |  1   5  1|
A = absolute value of:  1%2F2| -4   0  1|
`                         |-1%2F4-15%2F4 1|

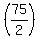A = absolute value of 1%2F2%2875%2F2%29 = 75%2F4

TRIANGLE's AREA = 75%2F4

Now we have to find the perimeter.

The side of the triangle between (1,5) and (-4,0) is

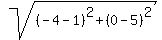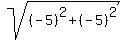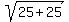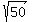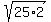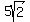D = sqrt%28%28-4-1%29%5E2%2B%280-5%29%5E2%29} = sqrt%28%28-5%29%5E2+%2B+%28-5%29%5E2%29 = sqrt%2825%2B25%29 = sqrt%2850%29 = sqrt%2825%2A2%29 = 5sqrt%282%29

The side of the triangle between (1,5) and (-1/4,-15/4) is

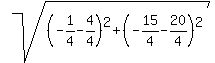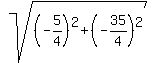D = sqrt%28%28-1%2F4-1%29%5E2%2B%28-15%2F4-5%29%5E2%29} = sqrt%28%28-1%2F4-4%2F4%29%5E2+%2B+%28-15%2F4-20%2F4%29%5E2%29 = sqrt%28%28-5%2F4%29%5E2%2B%28-35%2F4%29%5E2%29 =
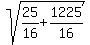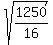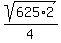sqrt%2825%2F16%2B1225%2F16%29 = sqrt%281250%2F16%29 = sqrt%281250%29%2F4 = sqrt%28625%2A2%29%2F4 = 25sqrt%282%29%2F4


The side of the triangle between (-4,0) and (-1/4,-15/4) is

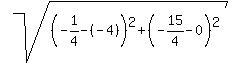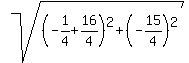D = sqrt%28%28-1%2F4-%28-4%29%29%5E2%2B%28-15%2F4-0%29%5E2%29} = sqrt%28%28-1%2F4%2B4%29%5E2+%2B+%28-15%2F4%29%5E2%29 = sqrt%28%28-1%2F4%2B16%2F4%29%5E2%2B%28-15%2F4%29%5E2%29 =
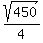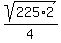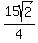sqrt%28%2815%2F4%29%5E2%2B225%2F16%29 = sqrt%28225%2F16+%2B+225%2F16%29 = sqrt%28450%2F16%29 = sqrt%28450%29%2F4 = sqrt%28225%2A2%29%2F4 = 15sqrt%282%29%2F4

So the perimeter is

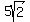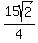5sqrt%282%29 + 25sqrt%282%29%2F4 + 15sqrt%282%29%2F4 =

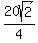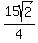20sqrt%282%29%2F4 + 25sqrt%282%29%2F4 + 15sqrt%282%29%2F4 =

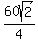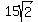60sqrt%282%29%2F4 = 15sqrt%282%29

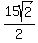One-half the perimeter (semiperimeter) = 15sqrt%282%29%2F2

Now we can use the formula:

                                           TRIANGLE'S AREA
RADIUS OF INSCRIBED CIRCLE OF TRIANGLE = --------------------
                                          HALF ITS PERIMETER

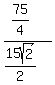RADIUS OF INSCRIBED CIRCLE OF TRIANGLE =%2875%2F4%29%2F%2815sqrt%282%29%2F2%29 
                                          
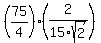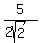RADIUS OF INSCRIBED CIRCLE OF TRIANGLE =%2875%2F4%29%282%2F15sqrt%282%29%29 = 5%2F%282sqrt%282%29%29 = %285sqrt%282%29%29%2F%282sqrt%282%29sqrt%282%29%29

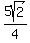RADIUS OF INSCRIBED CIRCLE OF TRIANGLE =5sqrt%282%29%2F4

Here's the graph:




Edwin