First we find the complementary solution of the
complementary homogeneous differential equation:
y''' + 4y' = 0
The auriliary polynomial equation is
r³ + 4r = 0
r(r²+4) = 0
r=0, r=±2i, which we think of as 
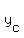
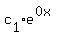
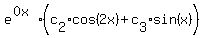
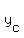
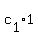
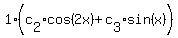
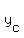
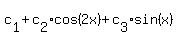Now we look for a particular solution to the original differential equation.
The right side is x + 3cos(x)
That would ordinarily make us think of this particular solution;
Ax + Bcos(x) + Csin(x)
We do not need a constant term because the complementary solution
already has c1.
However there is a "conflict" with the term x in the right side
and the term Ax in that choice for a particular solution. So we
must change that term by multiplying the term Ax by x, getting Ax².
That means we must still have a term in x. So we redo the assumed
particular solution to this:
yp = Ax² + Bx + Ccos(x) + Dsin(x)
yp' = 2Ax + B - Csin(x) + Dcos(x) [we can ignore the B, since we have c1]
yp" = 2A - Ccos(x) - Dsin(x) [we can ignore the 2A, since we have c1]
yp''' = Csin(x) - Dcos(x)
No we'll line up the terms of the original differential equation:
yp''' = Csin(x) - Dcos(x)
+4yp' = 8Ax - 4Csin(x) + 4Dcos(x)
--------------------------------------------------
x + 3cos(x) = 8Ax - 3Csin(x) + 3Dcos(x)
Equating coefficients of x: 1 = 8A, so A = 
Equating constants: 0 = 4B, so B=0
Equating coefficients of cos(x): 3 = 3D, so D = 1
Equating coefficients of sin(x): 0 = -3C, so C = 0
Particular solution:
yp = Ax² + Bx + Ccos(x) + Dsin(x)
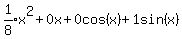yp = 
yp =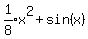 
General solution:
.
--------------------------------------
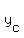
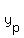
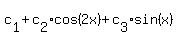
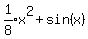If I have time I'll do the other one by variation of parameters later.
Edwin
