Question 844183: The figure below shows the graph of a rational function with vertical asymptotes x=1,x=5, and horizontal asymptote y=0. The graph does not have an x-intercept, and it passes through the point (3,1). Write in simple form
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Some help on the analysis:
The denominator contains factors, (x-1) and (x-5). These factors do not occur in the numerator. Between x=1 and x=5, the denominator becomes negative, but to the left of x=1 and to the right of x=5, the denominator is positive. You want a way for the rational expression to stay positive as described, "graph does not have an x-intercept" and contains "point (3,1)". A way to do this is have both binomial factors in the denominator, squared. This way, the rational expression is always positive; and the extreme left and right behavior will approach zero.
The function can be something, 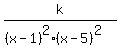 . .
You want to find k using the included point of (3,1).
At x=3, the expression must be 1. Find k.
|
|
|