Question 810931: Suppose you have a rectangular sheet with width of 5in and length of 10in. You want to make an open-top box from this sheet by cutting out squares from each corner and folding up the sides. Let the side of each square have length x in.
Find an expression in terms of x (in simplified form) of the surface area of the open-top box. Let the surface area be denoted by A(x).
Choose one:
a. A(x) = 100 - 30x
b. A(x) = 100 - 2x2
c. A(x) = 50 - 4x2
d. A(x) = 50 + 15x - 3x2
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The surface area of one side of the original rectangular sheet was
  .
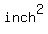(The other side had the same area, and the edges must have a very small surface, because that sheet must be very thin to be able to fold it).
The surface area of each square cut off, in square inches is 
The total surface area cut off is  .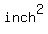
So the surface area of the outside surface of the box, in square inches, can be calculated as
 (answer c)
If you calculated the surface of the base and the sides and added them up, you would get the same answer, of course.
(It is just a lot more work).
The lengths of the sides of the base (in inches) are
length = 
width =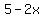 
That makes the surface of the base (in square inches) equal to
The perimeter of the base (in inches) is
The height of the sides of the base (in inches) is  .
WE can calculate the surface area of the sides of the box as perimeter of the base times height of the box to get
 .
Adding the surface of the base of the box to the surface of the sides of the box, we get the total surface area of the box, in square inches as
 which simplifies to
(answer c)
When you get the answer the hard way first,
and then realize that there was a much easier way,
showing both ways (as if you saw them both from the start),
and stating that one way is a more efficient way to the answer makes you look smart.
(I've done that).
If you show only the short way,
and someone insist that you must have done something wrong,
because they know that is not the proper way to solve the problem,
use your judgement and discretion. Be cautious.
You could argue (with some discretion and diplomacy) that there is nothing wrong with the shorter solution,
and that a shorter solution is a better solution.
(I've argued too, not always as cautiously as advisable).
However, it may be hard or impossible to convince a person who thinks the longer solution is the only correct solution.
It may not win you a friend, and there may be unpleasant consequences.
|
|
|
