Question 800872: What is a quick and easy way of solving algebraic equations?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! It depends on the type of equation.
That's the quick and short answer.
I'll give you a long answer.
Algebra is a language.
To use algebra you need to know the meaning of symbols and you need to know the rules for order of operations. Those rules are needed so we can understand one another.
To be understood in any language, you need to form sentences arranging words in a certain order. If you scramble the order of the words in a sentence, your meaning is likely to be misunderstood.
The simplest equations are equations like
 , which is the same as , which is the same as 
According to the rules for order of operations,
the expressions 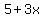 and and 
both mean that the value for  is first multiplied times 3, is first multiplied times 3,
and then 5 is added.
The equations say that the result of doing that is 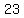 . .
To solve that equation (to get back to the value of  ), ),
you need to undo the steps in reverse order.
That's how things are usually undone in life.
You take off your shoes before you take of your socks,
undoing the putting on of socks and shoes in the reverse order.
So you transform the equation 
into  by undoing the adding of 5. by undoing the adding of 5.
That simplifies into  . .
The next step is undoing the multiplication times 3,
transforming  into into  ÷ ÷ , ,
which simplifies into  . .
At each step you can think of the equation as the two expressions on both sides of the equal sign being balanced on the pans of a two pan balance,
or on the two ends of a seesaw.
For the two sides to stay equal (balanced),
whatever you do to one side (the entire side),
you have to do to the other side.
From  we get to we get to  by subtracting 5 from both sides. by subtracting 5 from both sides.
I can write that in steps as



 , ,
or I can just write


You need to write as many steps as needed for your comfort and the teachers comfort.
NOTE:
It is a good idea to verify the solution you find.
To verify, you substitute your solution and see if it makes the original equation true.
To verify that  is the solution to is the solution to  , ,
I substitute  for for  in the expression in the expression  . .
It turns into
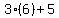 which is which is 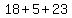 , so , so  makes the equation makes the equation  true. true.
That means that my solution is correct.
I did not make a mistake this time.
|
|
|