Question 78465: I need help with this problem. I hope I am in the right area for asking this question.
The electrical resistance R of a wire varies directly as its length L and inversely as the square of its diameter. A wire 20 meters long and 0.6 centimeters in diameter made from a certain alloy has a resistance of 36 ohms. What is the resistance of a piece of wire 60 meters long and 1.2 centimeters n diameter made from the same material?
a. 24 ohms
b. 27 ohms
c. 30 ohms
d. 48 ohms
thank you for you help
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem tells you that the resistance of a wire is directly proportional to its length
and inversely related to its cross sectional area. The cross sectional area of the circular
shape of the wire is  where r is the radius of the wire. where r is the radius of the wire.
.
Using this we can write an equation that says:
.

.
where R is the resistance of the wire, L is the length of the wire in meters, and r is
the radius of the cross sectional circle of the wire. k is a constant of proportionality.
It takes into consideration the material in the wire, the fact that length is in meters
for this problem, and also the fact that the cross sectional radius is in centimeters.
We don't know k, but we can find it.
.
We find k by taking the one case where for the wire we know the resistance. That case
says that L is 20 meters, r is 0.6 cm, and the resistance of that piece of wire is 36 ohms.
Substitute these values into the equation:
.

.

.
Solve this for k by dividing both sides by 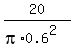 to get: to get:
.

.
When you divide the 36 by a fraction, it is equivalent to multiplying the 36 by the fraction
inverted. This says that the value of k is:
.

.
We can now use this value for k in the calculations we do for the 60 meter long wire. The
radius for that wire is 1.2 cm. The equation for the resistance of that wire is:
.

.
Now substitute the value for k to get:
.

.
Because the term  appears in both the numerator and the denominator, they cancel appears in both the numerator and the denominator, they cancel
each other. Also the 20 in the denominator goes into the 60 in the numerator 3 times.
These two changes reduce the equation to:
.

.
So the answer is that the resistance of the wire that is 60 meters long is 27 ohms,
and this is answer b in your list of answers.
.
Hope this helps you to understand the problem and how to solve it.
|
|
|