Question 757191: This question is based on grad 12, Calculus
a bacteria colony has a mass that varies with time.The original mass of the bacteria is 20 g and the mass increases by 50% eache day
a) write an equation to model the growth of the mass of the colony
b) what is the intial rate of change of the mass of the colony?
c) During which day is the mass of the colony increasing by 60 g/day?
d) When will the mass of the colony be 60 Kg?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The mass of the colony increases by a factor of 1.5 each day,
so if  = time elapsed, in days, = time elapsed, in days,
and  = mass of bacteria, in grams, = mass of bacteria, in grams,
we could write 
However, it is traditional (and more convenient when calculating derivatives) to use
 <-- answer to part a) of the problem <-- answer to part a) of the problem
b) The rate of change of the mass of the colony would be the derivative of 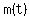

Fot  that rate is that rate is 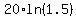 = approximately 8.1 g/day = approximately 8.1 g/day
c) During which day is the mass of the colony increasing by 60 g/day?
we need to find the value of  that makes the rate, that makes the rate,  , equal to 60 g/day , equal to 60 g/day
 --> -->  --> -->  --> -->  --> t = approx. --> t = approx. 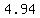 days. days.
I would call that time (and any time  between 4 and 5) day between 4 and 5) day  . .
d) When will the mass of the colony be 60 Kg?
60Kg is a lot. It's 60,000 grams.
 --> -->  --> -->  --> -->  --> -->  , so we approximate to , so we approximate to  . .
So, in the ideal world of math, it would take 20 days to get 60 kg of bacteria.
In real life, a colony would not keep growing at the same rate for that long. Even with a lot of attention, "feeding", and "transplanting", grow would not stay constant.
|
|
|