Question 73812: Find the slope of any line perpendicular to the line through points (3, 12) and (5, 4).
(A)–4 (B)4 (C)-1/4 (D)1/4
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! First find the slope of the line connecting the two points (3, 12) and (5, 4).
.
Recall that the slope is defined as the change in y values divided by the change in x values.
.
In going from point (3,12) to point (5,4) note that the value of x goes from +3 to +5, a
change of +2. Also in going from point (3,12) to point (5,4) note that y goes from +12
to +4, a change of -8.
.
Therefore, the slope, call it m, of this line is:
.

.
Once you have the slope of the line, you take the negative inverse of the slope and you have
the slope of the perpendicular line.
.
The inverse of -4 is 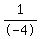 and the negative of that is and the negative of that is 
.
So answer D is the correct answer. The slope of the line perpendicular to the line that
joins the points (3,12) and (5,4) is  . .
.
Hope this helps. To find the slope of a perpendicular, first find the slope of the line and
then take the negative inverse of that slope. The inverse is found by dividing 1 by the slope
of the original line and once you find that inverse, multiply it by minus 1.
|
|
|