Question 696813: Find (a, b, c) if
2a+3b+c=11
6ab+2ac+3bc=24
abc=-6
Found 2 solutions by Alan3354, god2012:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find (a, b, c) if
2a+3b+c=11
6ab+2ac+3bc=24
abc=-6
-------------
Look for an integer solution
---
abc = -6 --> 1 negative # and they #'s are 1, 2 & 3
--------
c = -1
b = 2
a = 3
Answer by god2012(113)  (Show Source):
You can put this solution on YOUR website! 2a+3b+c=11 ---------------------------------eq.1
6ab+2ac+3bc=24-------------------------------eq.2
abc=-6 -------------------------------------eq.3
From Eq.1 , 2a+3b = 11 - c
From eq.2 , 6ab + c (11 - c) = 24
 ----------------------eq.4
From eq.3 , ab = -6/c
Therefore eq.4 becomes
 is a cubic equation
By trial and error , one of the roots of the equation is -1.
Therefore ,(c-1) is a factor.
Let us reduce the cubic equation to a quadratic equation.
We get , 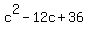 is the quotient which is a quadratic equation.
The roots are 6 and 6.
c = {-1,6}
Therefore 2a+3b = 11-(-1) = 12 --------------------eq.5
ab(-1) = -6
ab = 6
b = 6/a
Substitute for b in eq.5
 is a quadratic equation whose roots are 3 and 3
Therefore , b = 2
(a,b,c) = (3,2,-1) when c = -1
But when c = 6, we have 2 possibilities for a and b
(a,b,c) = (3,-1/3,6) OR (-1/2 , 2,6)
|
|
|
