

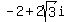
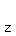

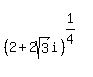
 ,
,  ,
,  =
=  =
= 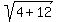 =
= 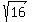 =
= 




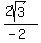

 .
The reference angle for
.
The reference angle for  is 60░ and since x is - and y is +,
is 60░ and since x is - and y is +,
 is in the 2nd quadrant, so we subtract 60░ from 180░ and get
120░, which has the same trig functions as 120░ + 360░Ěk, so we take:
is in the 2nd quadrant, so we subtract 60░ from 180░ and get
120░, which has the same trig functions as 120░ + 360░Ěk, so we take:


 .
Now we have
.
Now we have
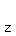

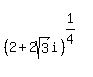

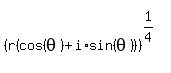

 Now we use the formula:
Now we use the formula: 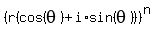

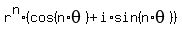
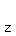






 Now we let k = 0,1,2,and 3 to get the 4 4th roots, the 4 possible
answers for z:
For k = 0,
Now we let k = 0,1,2,and 3 to get the 4 4th roots, the 4 possible
answers for z:
For k = 0,


 For k = 1,
For k = 1,


 For k = 2,
For k = 2,


 For k = 3,
For k = 3,


 Those are the four values for z.
Edwin
Those are the four values for z.
Edwin