Question 662229: How Many Oranges?
Marjorie, Colleen, and Bob picked oranges together. They were tired after picking a large number of oranges and so fell asleep. Marjorie woke first and decided to take her third of the oranges and head home. She counted the oranges, and found that the number was divisible by 3 if she took one of the oranges first. Marjorie took one orange and then took one-third of the remaining oranges. She left quietly.
Bob awoke a short time later, noticed that Colleen was sleeping, and presumed Marjorie had gone for a walk. He decided to head home because he wasn’t feeling well. Not realizing that anyone had left, he counted the oranges and found that the number of oranges was two more than a number that could be easily divided by 3. So he took the two extra oranges and then one-third of what was left. He left without waking Colleen and without waiting for Marjorie to return.
Colleen finally awoke and wondered where her friends had gone. She assumed they were both busy somewhere nearby. Before she left, she counted the oranges and was surprised at how small the number was. She found that the number of oranges was one more than a multiple of three, so she took the extra orange and one third of those remaining.
1. What was the total number of oranges the friends picked?
2. How many oranges were left behind when Colleen departed?
3. Is more than one answer possible for the total number of oranges? If so, what other numbers are possible? Explain.
4. Based on the values you found in problem 3, determine a reasonable solution to the problem. Explain your answer.
5. Is it possible that five oranges remained after Colleen took her “share”? Explain.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAIMER:
I do not know how you were expected to solve the problem.
I do not know if there is a much simpler way to solve it.
MY IDEAS FOR A SOLUTION:
Colleen found a number of oranges that was one more than a multiple of 3.
Let's call that number 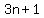 with with  being a positive integer. being a positive integer.
Colleen took  , which was , which was  plus 1/3 of plus 1/3 of  , leaving , leaving  . .
From here on, I get into cumbersome algebra expressions with  , ,
but you could start trying values for  instead, and work with numbers. instead, and work with numbers.
That 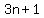 Colleen found, is the number of oranges Bob left. Colleen found, is the number of oranges Bob left.
Bob meant to leave  for Colleen and for Colleen and  for Marjorie, for Marjorie,
after he took another  plus plus  extra for himself. extra for himself.
In other words, the 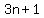 was 2/3 of the oranges left after Bob took his extra was 2/3 of the oranges left after Bob took his extra  oranges. oranges.
On waking up, Bob had found
 oranges. oranges.
That was what Marjorie had left, and was 2/3 of what was there
right after Marjorie took the first orange.
On waking up, Marjorie had found 3/2 as many, plus 1, or
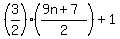 oranges. oranges.

That was  , the total number of oranges the friends had picked: , the total number of oranges the friends had picked:
 <--> <--> 
At this point, we can try numbers for  , ,
and check if 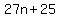 is a multiple of 4. is a multiple of 4.
It has to be, because  should be an integer. should be an integer.
We could find that it works for  values of values of  , ,  , ,  , and so on, , and so on,
while the values for  are are 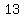 , , 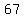 , and so on. , and so on.
We may start to see a pattern, and find a general formula for the infinite possible values of  . .
Alternatively, working from  , we can find that , we can find that
 --> -->  --> -->  --> -->  --> -->  --> --> 
That tells you that 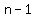 must be a multiple of 4 (or zero). must be a multiple of 4 (or zero).
In other words  <--> <-->  with with  a non-negative integer. a non-negative integer.
Substituting,
 --> -->  --> -->  --> --> 
1.  with with  a non-negative integer. a non-negative integer.
(that gives you 13, 40, 67, and so on, just keep adding 27)
2. When Colleen departed there were  oranges left. oranges left.
That could be 2, or 10, or 18, or 26, or ...
3. There are potentially infinity of answers, but I would believe not too many.
It all depends on Colleen's idea of a small number. Collen counted the oranges and was surprised at how small that number was. oranges and was surprised at how small that number was.
No telling what Colleen thinks is a small number.
Maybe  is a small number to Colleen. is a small number to Colleen.
Maybe 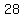 is a large number to Colleen, and the small number she counted was is a large number to Colleen, and the small number she counted was
 or or  . .
Maybe Colleen expected more oranges, and finding
 , she thought that was a small number. , she thought that was a small number.
4. I'd say Collen counted  , for , for  , ,
which makes  --> --> 
5. Colleen took 1 orange first, to make the rest be 3 equal shares.
When, after that, Colleen took 1 of those 3 equal shares, she left 2 equal shares,
so the number left should have been an even number.
It could not have been 5.
|
|
|