Question 661525: solve (12x/x-4) - (3x^2/x+4)= (384/x^2-16)
Found 2 solutions by ReadingBoosters, MathTherapy:
Answer by ReadingBoosters(3246)   (Show Source): (Show Source):
You can put this solution on YOUR website! (12x/x-4) - (3x^2/x+4) = (384/x^2-16)
Factor the right
384 / (x+4)(x-4)
(12x/x-4) - (3x^2/x+4) = (384/(x+4)(x-4))
Multiply both sides by (x+4)
(12x(x+4)/x-4) - 3x^2 = 384/(x-4)
Multiply both sides by (x-4)
12x(x+4) - 3x^2(x-4) = 384
12x^2 + 48x - 3x^3 + 12x^2 = 384
24x^2 + 48x - 3x^3 = 384
3x(-x^2 + 8x + 16) = 384
Divide both sides by 3
x(-x^2 + 8x + 16) = 128
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
solve (12x/x-4) - (3x^2/x+4)= (384/x^2-16)


 ----- Multiplying by LCD, (x - 4)(x + 4) ----- Multiplying by LCD, (x - 4)(x + 4)


 ------ Factoring out GCF, - 3 ------ Factoring out GCF, - 3

Trying factors of + 128, we can see that one of the roots (solutions) of this equation is 4. Therefore, x - 4 is a factor of this equation.
Dividing the equation,  by (x - 4), we get: by (x - 4), we get: 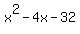 , and this factors to: (x - 8)(x + 4). , and this factors to: (x - 8)(x + 4).
Therefore,  becomes: becomes:  . This means that: . This means that:
x - 4 = 0

x - 8 = 0

x + 4 = 0

However, 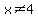 , or , or  , as either will make the equation UNDEFINED. Therefore, only solution is: , as either will make the equation UNDEFINED. Therefore, only solution is: 
After doing all this work, I'm sure you can do the check!!
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|