SOLUTION: Find the center (h, k) and the radius r of the circle 3x^2+7x+3y^2-7y-5=0

Algebra ->  Equations -> SOLUTION: Find the center (h, k) and the radius r of the circle 3x^2+7x+3y^2-7y-5=0      Log On


   

Question 660817: Find the center (h, k) and the radius r of the circle
3x^2+7x+3y^2-7y-5=0
Answer by math-vortex(648) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, there--

Problem:
Find the center (h, k) and the radius r of the circle
3x%5E2%2B7x%2B3y%5E2-7y-5=0

Answer:
We want to rearrange this equation into the form (x-h)^2 +(y-k)^2 = r^2. Then we can read the center point and the radius right off the equation.

Divide every term in the equation by 3, so that the x-squared and y-squared terms have a coefficient of 1.

x%5E2%2B%287%2F3%29x%2By%5E2-%287%2F3%29y-5%2F3=0

Add 5/3 to both sides of the equation.
x%5E2+%2B+%287%2F3%29x+%2B+y%5E2-%287%2F3%29y+=+5%2F3

Complete the square for the x terms by adding a constant. To make a perfect square trinomial find half the coefficient of the x-term and square it. Half of 7/3 is 7/6. Th square of 7/6 is 49/36. Add this to both sides of the equation.
%28x%5E2%2B%287%2F3%29x%2B49%2F36%29+%2B+y%5E2+-%287%2F3%29y=5%2F3%2B49%2F36

Repeat this process for the y-terms.


Write each trinomial in factored form. Sum up the constants on the right side.
%28x%2B7%2F6%29%5E2%2B%28y-7%2F6%29%5E2=158%2F36

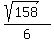The square root of 158/36 is %28sqrt%28158%29%29%2F6 because the square root of 36 is 6. THe final equation is 

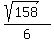%28x%2B7%2F6%29%5E2%2B%28y-7%2F6%29%5E2=%28%28sqrt%28158%29%29%2F6%29%5E2

The center of the circle is the point (h,k)=(-7/6, 7/6)
The radius of the circle is %28sqrt%28158%29%29%2F6

Hope this helps! Feel free to email if my explanation is unclear or you have additional questions.

Mrs.Figgy
math.in.the.vortex@gmail.com