SOLUTION: f(x)= x2-9over x2-5x-14

Algebra ->  Equations -> SOLUTION: f(x)= x2-9over x2-5x-14      Log On


   

Question 64954: f(x)= x2-9over x2-5x-14
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
f(x)= x2-9over x2-5x-14
f(x)=[(x-3)(x+3)]/[x^2-5x-14]
f(x)=[(x-3)(x+3)]/[(x-7)(x+2)]
Cheers,
Stan H.

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!

           xｲ - 9
f(x) = 覧覧覧覧覧覧覧
        xｲ - 5x - 14

So? What do you want us to do with it?  You forgot to give us
any instructions. Next time you post a problem, be sure to
give the instructions as to what is supposed to be done.  Don't
just give the equation or expression without telling us what to
do with it.  Otherwise all we can do is guess.

Do you want to find all the vertical and horizontal asymptotes,
find the domain and range and draw the graph?  I'll guess that's 
what you want.

To find the equations of the vertical asymptotes by setting the 
denominator = 0 and solving for x:

  xｲ - 5x - 14 = 0
(x - 7)(x + 2) = 0

Setting x-7=0 gives x = 7 
Setting x+2=0 gives x = -2

x = 7 and x = -2 are equations of two vertical lines which are the
the asymptotes.  You should begin by drawing them in like this:

graph%28300%2C166.7%2C-7%2C11%2C-5%2C5%2C999%28x%2B2%29%2C999%28x-7%29+%29


Since there are asymptotes at -2 and 7, the domain of the function
does not include them.  However any other value of x is in the
domain, so the domain is 

(-･, -2) ﾈ (-2, 7) ﾈ (7, ･)

Now we can find the horizontal asymptote by using the rules:

1. If the degree of the numerator is greater than the degree of the
   denominator, then there is no horizontal asymptote.
2. If the degree of the numerator is less than the degree of the
   numerator, then the horizontal asymptote is the x-axis, whose
   equation is y = 0.
3. If the degrees of the numerator and the denominato are the same
   then the equation of the horizontal asymptote is 
   y = (leading coeff of numerator)/(leading coeff of denominator)

In f(x), we have the 3rd case, so the horizontal asymptote has
equation y = 1/1 or y = 1.  

So we draw in the horizontal asymptote:

graph%28300%2C166.7%2C-7%2C11%2C-5%2C5%2C999%28x%2B2%29%2C999%28x-7%29%2C1%29+%29

Now we get a few points, say (-5, 4/9), (-4, 7/22), (-3,0), (-1,1), 
(1,4/9), (2, 1/4), (3,0), (6,-3 3/8), (8, 5 1/2) 



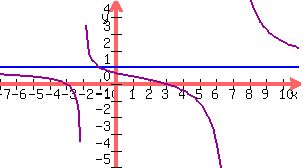Now to find the range.  Oftentimes we have to omit the value of y 
where there is a horizontal asymptote from the range.  However, this 
is one of the unusual cases of a graph which crosses its horizontal 
asymptote y=1 at the point (-1,1). So we cannot rule out any number 
in the range, and so the range of f(x) is (-･, ･).

Hopefully something is here that you were looking for.  If not, post 
again, giving the instructions as to what you are supposed to do 
with f(x).

Edwin