Question 638414: Rational Equations. Solve the equation.
(2x-9)/(x-7)+x/2=5/(x-7)
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! to solve for x, you will first need to find the LCD of the fractions involved. Let's look at the denominators: x - 7, 2, x - 7. The LCD of these fractions is 2(x - 7). We will then multiply each fraction by 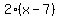 : :
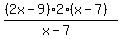 + +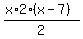 = =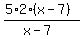
Since we can cancel out the same terms from both the numerator and denominator of each fraction, we are left with:
 = =
 = =

If we subtract the 10 on the right side of the equal sign, from both sides, we are left with a quadratic equation:

Let's see if we can solve this equation by factoring. We need to find out if any numbers that will multiply together and produce -28, can be added together to equal -3: 4 x -7= 28 and when we add 4 to -7, we get -3. So, turning this equation into factors, we get (x - 7)(x + 4) = 0, which means x = 7 and/or x = -4. Since we are unsure if either or both will work, we will have to substitute 7 and -4 for x in our original equation. Uh oh. Look at the first fraction in our equation. The denominator is x - 7. If we plug our 7 in for x, our denominator will equal 0. Denominators cannot equal 0, therefore, we know right away that 7 cannot be one of our solutions.
Now, let's try -4:
 = =
 = =

The LCD of our remaining fractions is 11, so we would multiply 11 by each of our fractions by 11, which would leave us with the following:
 = =

since both sides of the equal sign are the same, we know that -4 is a solution.
Final Answer: x = -4
|
|
|