Question 61781: When solving a rational equation, why it is OK to remove the denominator by multiplying both sides by the LCD and why can you not do the same operation when simplifying a rational expression?
Answer by mathick(4)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Good question. The difference between expressions and equations is key to the answer.
A simple example of an expression is:  . .
And a simple example of an equation is:  . .
If the equation were a scale, the left side and right side would balance each other perfectly. Now if the same weight (say 3) is added to both sides of the equation:
 , ,
you get an equation that is equivalent to (basically the same as) the original equation  . .
 is basically the same equation as is basically the same equation as  (they have the same answer). (they have the same answer).
In an equation, the left and right side are balanced. The main idea in solving equations is: if you start with a balanced scale and then do the same thing to both sides of the scale, the scale will still end up balanced.
With an expression, however there's no scale. An expression is like a weight just sitting there on it's own. So if 3 is added to an expression, it's no longer the same expression.
 is not the same expression as is not the same expression as 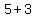 . .
Moving to your question, the reason you can multiply both sides of  by 6 is that you're preserving the balance by doing the same thing (multiplying by 6) to both sides. by 6 is that you're preserving the balance by doing the same thing (multiplying by 6) to both sides.
Multiplying the expression 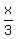 by 6, however, results in a different expression that's not equivalent. So multiplying an expression by a number typically changes the expression and so isn't allowed. by 6, however, results in a different expression that's not equivalent. So multiplying an expression by a number typically changes the expression and so isn't allowed.
Sometimes, though you do multiply an expression by 1. Multiplying by any other number usually changes the expression, but multiplying by 1 doesn't change it. That's why multiplying by 1 is allowed. Usually you multiply by 1 in a different form, such as  or or 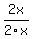 . For example, starting with . For example, starting with
 , ,
you can multiply the 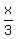 by by 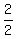 and the and the  by by  : :

to get the common denominator:
 . .
I hope this helps - let me know if you have questions about any part of it.
|
|
|