Question 54925: P and Q are whole numbers such that 0
I have absolutely no idea. I don't really understand the way the problem was worded. It would be great if I had some help!
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is actually a neat problem. Before we begin, are we allowed to use unreduced fractions? For example, one solution is 2/3, but also you could use 6/9, which has the same value. Do these both count? I think they do.
So, begin with the values of P and Q, which are as follows:
P=1, P=2, P=3,P=4, P=5, P=6, P=7, P=8, P=9
Q=1, Q=2, Q=3,Q=4, Q=5, Q=6, Q=7, Q=8, Q=9
The ratio of these numbers  must be between must be between 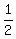 and and  , not including ratios that are equal to , not including ratios that are equal to  or or  . .
Start with P=1, and try 1/1, 1/2, 1/3, etc. down to 1/9. None of these work.
Now, try P=2: 2/1 and 2/2 do not work. NOTE THAT 2/3 works, but 2/4, 2/5, etc do not work.
Now, try P=3: 3/1, 3/2, and 3/3 do NOT work. NOTE THAT 3/4, 3/5 work, but none of the rest will work.
Now, try P=4: 4/1, 4/2, 4/3, and 4/4 do NOT work. NOTE THAT 4/5, 4/6, 4/7 work, but the rest do not work.
Now, try P=5: Are you getting the pattern? The ones that work are 5/6, 5/7, 5/8, and 5/9.
For P=6: 6/7, 6/8, and 6/9
For P=7: 7/8, and 7/9
For P=8: 8/9
For P=9: None work.
Summary:  , ,  , ,  , ,  , , 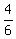 , ,  , , , , , , 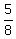 , ,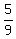 , , 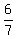 , ,  , ,  , ,  , ,  , , 
I counted 16 such numbers, including both fractions that reduce and those that do not reduce.
R^2 at SCC
|
|
|