Question 547547: Help solve please: 3/2x - x/4x^2-1 = 7/4x+2
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 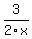 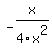  ? That would be way to simple.
You probably meant 3/2x - x/(4x^2-1) = 7/(4x+2), which I can write as
 .
The first thing to do is looking for factors in the denominators. I can factor them, to get:
A good common denominator would be 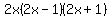 , but instead of writing denominators over and over I will multiply both sides of the equation by that expression to eliminate denominators.
 , which simplifies to
Multiplying as indicated, we get
 --> 
Adding  to both sides, we get 
Whichever way you solve that quadratic equation (factoring, completing the square, or applying the quadratic formula), you get the two solutions
 and 
It's a good idea to check, because, even if we make no mistakes, on eliminating denominators we can introduce extraneous solutions, that were not solutions of the original equation because they made one of the denominators zero. Our solutions do not make any of the denominators zero, but I often make mistakes, so I'll verify the solutions.
For ,  and 
For ,  and 
Both solutions work.
|
|
|
