Question 507817: The formula V=1/3lwh relates the volume of a square pyramid to its base length l, base width w, and height h.
a. Solve the formula for w
b. A square pyramid has a volume of 560 in^3, a base length of 10 in, and a height of 14 in. What is its base width?
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula:
 Relates to any "rectangular" pyramid, of which, a "square" pyramid is an example. Relates to any "rectangular" pyramid, of which, a "square" pyramid is an example.
To say "square" pyramid implies that the base is a square where the length, l, and the width, w. are equal.
Anyway, back to the given problem!
a) Solve for w:
 Multiply both sides by 3. Multiply both sides by 3.
 Now divide both sides by Now divide both sides by 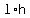
 or or 
b) A "square" pyramid has a volumre of 560 sq.in, a base length of 10 in., and a height of 14 in. FInd the width of the base.
(If it were truly a "square" pyramid, the width would be 10 in.)
Let's apply the formula we just derived for w:
 Substitute V = 560, l = 10, and h = 14. Substitute V = 560, l = 10, and h = 14.
 Evaluate. Evaluate.

 in. in.
|
|
|