I. 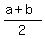 NO, because
NO, because 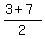 =
=  = 5, which is ODD
II.
= 5, which is ODD
II. 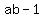 YES, because an ODD times an ODD is an ODD,
so ab is always ODD, and then when we subtract 1 from that ODD,
we will always get an EVEN.
or algebraically,
(2m+1)(2n+1)-1 = 4mn+2m+2n+1-1 = 2(2mn+m+n) = which is EVEN.
III.
YES, because an ODD times an ODD is an ODD,
so ab is always ODD, and then when we subtract 1 from that ODD,
we will always get an EVEN.
or algebraically,
(2m+1)(2n+1)-1 = 4mn+2m+2n+1-1 = 2(2mn+m+n) = which is EVEN.
III. 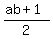 NO, because
NO, because  = 11, which is ODD
Therefore only II is always even. Answer b.
Edwin
= 11, which is ODD
Therefore only II is always even. Answer b.
Edwin