SOLUTION: If {{{1/x+1/y=1/(2z)}}} then z is equal to ? I know the answer is {{{xy/(2(x+y))}}}. Please explain the method. Thanks!

Algebra ->  Equations -> SOLUTION: If {{{1/x+1/y=1/(2z)}}} then z is equal to ? I know the answer is {{{xy/(2(x+y))}}}. Please explain the method. Thanks!       Log On


   

Question 460138: If 1%2Fx%2B1%2Fy=1%2F%282z%29 then z is equal to ? I know the answer is xy%2F%282%28x%2By%29%29. Please explain the method. Thanks!
Found 2 solutions by Edwin McCravy, richard1234:
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
1%2Fx%2B1%2Fy=1%2F%282z%29
We must clear of fractions. The denominators are x, y, and 2z.
They have no common factors so the LCD is their product 2xyz.
So we multiply all terms on both sides by 2xyz, which I will 
write as 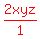red%282xyz%2F1%29



Now we will cancel all that will cancel:



2yz%2B2xz=xy

Factor 2z out of the two terms on the the left side:

2z%28y%2Bx%29=xy

To solve for z, divide both sides by 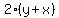2%28y%2Bx%29

%282z%28y%2Bx%29%29%2F%282%28y%2Bx%29%29=%28xy%29%2F%282%28y%2Bx%29%29

Cancel on the left:



z=xy%2F%282%28y%2Bx%29%29

It is customary to keep alphabetical order, so
we write y+x as x+y

z=xy%2F%282%28x%2By%29%29

Edwin

Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
We can write the left side as one fraction:



This is equal to 1/2z, so



Cross multiply:



Divide both sides by 2(x+y) and we get our final result

.