Question 454369: Write an equation of the line containing the given point and parallel to the given line. Express your answer in the form y=mx+b
(-6,7); 2x=9y+8
Found 3 solutions by mananth, solver91311, ikleyn:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2x-9y=8
Find the slope of this line
-9y=-2x +8
Divide by -9
y = 0.22 x + -0.89
Compare this equation with y=mx+b
slope m = 0.22
The slope of a line parallel to the above line will be the same
The slope of the required line will be 0.22
m= 0.22 ,point (-6,7)
Find b by plugging the values of m & the point in
y=mx+b
7=-1.33+ b
b=8.33
m=0.22
Plug value of the slope and b
The required equation is y=0.22 x+8.33
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(53547)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write an equation of the line containing the given point and parallel to the given line.
Express your answer in the form y=mx+b
(-6,7); 2x=9y+8
~~~~~~~~~~~~~~~~~~~~~~~~
The solution and the answer in the post by @mananth both are incorrect.
They are incorrect, since @mananth permanently rounds rational fractions to decimal fractions
even when it is not allowed and ruins the precise form of equations.
So, I came to make the job in a right way as it SHOULD be done.
Any line parallel to 2x = 9y + 8 has the form
2x = 9y + c, (1)
where 'c' is a real constant. To find 'c', we simply insert coordinates (-6,7) into equation (1)
2*(-6) = 9*7 + c,
-12 - 63 = c,
c = -75.
Thus equation (1) takes the form
2x = 9y - 75. (2)
To get the form y = mx + b, we express 'y' from equation (2)
y = 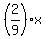 + +  ,
or, which is the same
y = ,
or, which is the same
y = 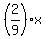 + 8 + 8 . (3)
So, the slope of the sough line is m = . (3)
So, the slope of the sough line is m =  and its equation is y = and its equation is y = 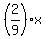 + 8 + 8 . .
Solved correctly.
|
|
|