Question 451061: Write an equation of the line containing the given point and parallel to the given line. Express your answer in the form Y=MX+b.
(-3,3);4x=5y+6
The equation of the line is Y=
(Simplify your answer. Use integers or fractions for any numbers in the expression)
Found 3 solutions by mananth, ikleyn, josgarithmetic:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! (-3,3);4x=5y+6
-5y=-4x+6
Divide by-5
y=0.8x-1.2
Compare this equation with y=mx+b
slope m =0.8
The slope of a line parallel to the above line will be the same
The slope of the required line will be 0.8
m=0.8,point(-3, 3)
Find b by plugging the values of m & the point in
y=mx+b
3=-2.40 +b
b=5.4
m=0.8
Plug value of the slope and b
The required equation is y=0.8x+ 5.4
Answer by ikleyn(53547)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write an equation of the line containing the given point and parallel to the given line.
Express your answer in the form Y=MX+b.
(-3,3);4x=5y+6
The equation of the line is Y=
(Simplify your answer. Use integers or fractions for any numbers in the expression)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A standard consideration and treatment for this case is as follows.
Any line parallel to the line 4x = 5y + 6 has the form 4x = 5y + c,
where 'c' is some constant.
So, the only thing we should do to solve the problem is to find
this constant 'c' from this equation. For this, we substitute the coordinates
of the given point into this equation
4*(-3) = 5*3 + c,
-12 = 15 + c,
c = -12 - 15 = -27.
Thus the sought equation is
4x = 5y - 27.
If you want it in the slope-intercept form, express 'y'
y = 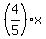 + 5.4. + 5.4.
That is all. At this point, the problem is solved completely.
Answer by josgarithmetic(39713)   (Show Source): (Show Source):
|
|
|