Question 447396: I need help writing the slope-intercept equation for the line that passes through (-3, -15) and is perpendicular to -6x + 8y = 3. Thank you.
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! (-3, -15) and is perpendicular to -6x + 8y = 3. Thank you.
-6x+8y = 3
Find the slope of this line
8y=6x-3
Divide by 8
y= 3/4x-0.38
Compare this equation with y=mx+b
slope m =0.75
The slope of a line perpendicular to the above line will be the negative reciprocal = -1.33
(m1*m2=-1) m=
-1.33 ,point( -3,-15)
Find b by plugging the values of m & the point in
y=mx+b
-15=4.00 +b
b=-19
m=-1.33
The required equation is y=-1.33x -19
m.ananth@hotmail.ca
Answer by ikleyn(53547)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need help writing the slope-intercept equation for the line that passes through (-3, -15)
and is perpendicular to -6x + 8y = 3. Thank you.
~~~~~~~~~~~~~~~~~~~~~
The " solution " in the post by @mananth is INCORRECT.
Speaking in soft manner, it is absurdist, since he identifies the values -4/3 and -1.33,
although they are absolutely different, as any 5th grade student knows.
Therefore, I will re-write his solution to present it in correct form.
Your starting equation is
-6x + 8y = 3.
Find the slope of this line
m1 =  = =  .
The slope of a line perpendicular to the above line will be the negative reciprocal m2 = .
The slope of a line perpendicular to the above line will be the negative reciprocal m2 =  .
Now we want to write an equation of a straight line with the slope m2 = .
Now we want to write an equation of a straight line with the slope m2 =  through point (-3,-15).
Write it in the form
y = through point (-3,-15).
Write it in the form
y = 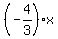 + b.
We need to find a constant 'b'.
Find 'b' by plugging the values of x = -3, y = -15
-15 = {{(-4/3)*(-3)}}} + b
-15 = 4 + b
b = -19
The required equation is y = + b.
We need to find a constant 'b'.
Find 'b' by plugging the values of x = -3, y = -15
-15 = {{(-4/3)*(-3)}}} + b
-15 = 4 + b
b = -19
The required equation is y = 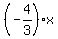 - 19. ANSWER - 19. ANSWER
Solved correctly.
In this kind of problems, @mananth runs his computer code, which generates
incorrect solutions every time, from problem to problem.
I just tired to disprove them.
|
|
|