Question 41512: Hello!
Can anyone help please?
My question is:
A woman has four dresses for which she paid a total of $80. The first dress cost as much as the second plus
half of the third. The second cost as much as the fourth minus the cost of the third. The third cost one-third
of the first. The fourth cost as much as the second and third together.
What was the price of each dress?
Thanks
marangeo
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the cost of the respective dresses be $w, $x, $y & $z.
Sum of the prices of all dresses = $80.
or w + x + y + z = 80 _______________(1)
Cost of first dress = cost of second +  cost of third cost of third
or w = x + 
or 2w = 2x + y ____________(2)
Cost of second dress = cost of fourth - cost of third
or x = z - y
or z = x + y______________(3)
Cost of third dress =  cost of the first cost of the first
or y =  w w
or w = 3y _________(4)
Substituting the expression for w from (4) in (1) and (2) we have, respectively,
x + 4y + z = 80 _________(5)
2x = 5y _____(6)
Substituting the expression of z from (3) in (5) we have
2x + 5y = 80 _______(7)
Now we have 2 equations with 2 unknowns.
2x = 5y _______(6)
2x + 5y = 80 __________(7)
Subtracting (6) from (7), we have
5y = 80 - 5y
or 10y = 80
or y = 8
From (4), w = 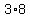 = 24 = 24
From (6), x = 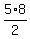 = 20 = 20
From (3), z = 20 + 8 = 28
Thus the costs of the 1st, 2nd, 3rd and 4th dress are $24, $20, $8 and $28 respectively.
V.V.I.
The last condition which states that the fourth dress cost as much as the second and third together is redundant. This means that this condition is not necessary to solve this problem. This problem involves 4 unknowns viz. w, x, y & z. So 4 equations have to be framed to solve for the unknowns. The first 4 conditions gives us 4 different equations and so the 5th or the last one is redundant. However, you may verify, after solving the problem, that the redundant 5th condition is also satisfied.
|
|
|