Question 40064This question is from textbook Aplied Algebra & Trig
: It has been 20+ years and algebra still makes me phisically sick. I am stumped on the silliest of things.
1/3(2a-8)-7 = 2/5a
The common denominator (as far as I can tell) is 15, then each term gets * by the common denom...
so does that mean?
15/3(30a-8)-105 = 15/5a
This question is from textbook Aplied Algebra & Trig
Answer by atif.muhammad(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
 Make the denominator of
Make the denominator of 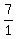 the same as the denominator of the same as the denominator of  .
Just times .
Just times 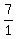 but some number to get its denominator to 3. In this case, we just times 1 (the denominator by 3 in order to get its overall denominator to 3.
Whatever we do the the denominator, must also be done to the numerator. We have times the denominator by 3 and therefore, we must also times the numerator by 3.
We end up with but some number to get its denominator to 3. In this case, we just times 1 (the denominator by 3 in order to get its overall denominator to 3.
Whatever we do the the denominator, must also be done to the numerator. We have times the denominator by 3 and therefore, we must also times the numerator by 3.
We end up with 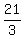 Now we have:
Now we have:
 We can join up the fractions on the left hand side as they have common denominators.
We can join up the fractions on the left hand side as they have common denominators.
 This gives us:
This gives us:
 Whenever we get this in maths, (a technique I have always used), we cross multiply.
So from,
Whenever we get this in maths, (a technique I have always used), we cross multiply.
So from,  We get,
We get,
 We can now multiply out the brackets.
We can now multiply out the brackets.
 Rearrange the equation:
Rearrange the equation:
 This is a quadratic equation.
This is a quadratic equation.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:
 For these solutions to exist, the discriminant
For these solutions to exist, the discriminant  should not be a negative number.
First, we need to compute the discriminant should not be a negative number.
First, we need to compute the discriminant  : :  .
Discriminant d=21265 is greater than zero. That means that there are two solutions: .
Discriminant d=21265 is greater than zero. That means that there are two solutions:  . .

 Quadratic expression
Quadratic expression 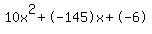 can be factored: can be factored:
 Again, the answer is: 14.5412618935271, -0.0412618935270729.
Here's your graph:
Again, the answer is: 14.5412618935271, -0.0412618935270729.
Here's your graph:
 |
x = 14.5412618935271, -0.0412618935270729
|
|
|