SOLUTION: what is the factored form of 4k^3-13k^2-12k

Algebra ->  Equations -> SOLUTION: what is the factored form of 4k^3-13k^2-12k      Log On


   

Question 387109: what is the factored form of 4k^3-13k^2-12k
Found 2 solutions by jim_thompson5910, tara0066:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

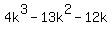4k%5E3-13k%5E2-12k Start with the given expression.


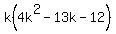k%284k%5E2-13k-12%29 Factor out the GCF k.


Now let's try to factor the inner expression 4k%5E2-13k-12


---------------------------------------------------------------


Looking at the expression 4k%5E2-13k-12, we can see that the first coefficient is 4, the second coefficient is -13, and the last term is -12.


Now multiply the first coefficient 4 by the last term -12 to get %284%29%28-12%29=-48.


Now the question is: what two whole numbers multiply to -48 (the previous product) and add to the second coefficient -13?


To find these two numbers, we need to list all of the factors of -48 (the previous product).


Factors of -48:
1,2,3,4,6,8,12,16,24,48
-1,-2,-3,-4,-6,-8,-12,-16,-24,-48


Note: list the negative of each factor. This will allow us to find all possible combinations.


These factors pair up and multiply to -48.
1*(-48) = -48
2*(-24) = -48
3*(-16) = -48
4*(-12) = -48
6*(-8) = -48
(-1)*(48) = -48
(-2)*(24) = -48
(-3)*(16) = -48
(-4)*(12) = -48
(-6)*(8) = -48

Now let's add up each pair of factors to see if one pair adds to the middle coefficient -13:


First NumberSecond NumberSum
1-481+(-48)=-47
2-242+(-24)=-22
3-163+(-16)=-13
4-124+(-12)=-8
6-86+(-8)=-2
-148-1+48=47
-224-2+24=22
-316-3+16=13
-412-4+12=8
-68-6+8=2



From the table, we can see that the two numbers 3 and -16 add to -13 (the middle coefficient).


So the two numbers 3 and -16 both multiply to -48 and add to -13


Now replace the middle term -13k with 3k-16k. Remember, 3 and -16 add to -13. So this shows us that 3k-16k=-13k.


4k%5E2%2Bhighlight%283k-16k%29-12 Replace the second term -13k with 3k-16k.


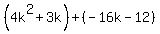%284k%5E2%2B3k%29%2B%28-16k-12%29 Group the terms into two pairs.


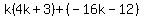k%284k%2B3%29%2B%28-16k-12%29 Factor out the GCF k from the first group.


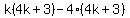k%284k%2B3%29-4%284k%2B3%29 Factor out 4 from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.


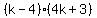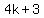
%28k-4%29%284k%2B3%29 Combine like terms. Or factor out the common term 4k%2B3


--------------------------------------------------


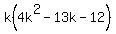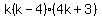
So k%284k%5E2-13k-12%29 then factors further to k%28k-4%29%284k%2B3%29


===============================================================


Answer:


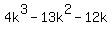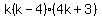So 4k%5E3-13k%5E2-12k completely factors to k%28k-4%29%284k%2B3%29.


In other words, 4k%5E3-13k%5E2-12k=k%28k-4%29%284k%2B3%29.


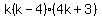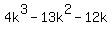Note: you can check the answer by expanding k%28k-4%29%284k%2B3%29 to get 4k%5E3-13k%5E2-12k or by graphing the original expression and the answer (the two graphs should be identical).


If you need more help, email me at jim_thompson5910@hotmail.com

Also, feel free to check out my tutoring website

Jim

Answer by tara0066(31) About Me  (Show Source):
You can put this solution on YOUR website!
k(4k^2-13k-12) Pull out what they have in common, in this case a k
Multiply your first value (4) and last value (-12). Find a number that multiplies to get -48 and their sum comes to -13 (which is your middle term).
3(-16) works for both situations.
k[4k^2-16k+3k-12] Replaced middle term with the values you found. Order doesn't matter.
k[4k(k-4)+3(k-4)] Split the 4 terms into two sets and pull out what the pairs have in common. Your two parenthesis inside should always match if you did this right.
k(k-4)(4k+3) Write the repeated set once and the other set comes from the values that you factored out. Don't forget the k from the beginning that was pulled out. It is still out there.
Hard to follow this one. A little complicated. Hope you could stay with me. lol. Good luck.