Question 241588: Simplify. Assume that no denominator is zero and that 0^0 is not considered. thanks
(a7/-7b^4) ^6
Found 2 solutions by stanbon, Alan3354:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Assume that no denominator is zero and that 0^0 is not considered. thanks
(a^7/-7b^4)^6
---
(a^42)/(117649b^24)
=======================
Cheers,
Stan H.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! 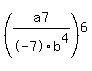 Is that a7 a^7? Is that a7 a^7?
= 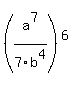 for some reason the minus sign caused a problem for some reason the minus sign caused a problem
= 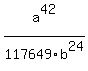
-------------
Note: by convention, 
-----------------------
The following is a list of reasons why 0^0 should be 1.
Rotando & Korn show that if f and g are real functions that vanish at the origin and are analytic at 0 (infinitely differentiable is not sufficient), then f(x)^g(x) approaches 1 as x approaches 0 from the right.
From Concrete Mathematics p.162 (R. Graham, D. Knuth, O. Patashnik):
Some textbooks leave the quantity 0^0 undefined, because the functions 0^x and x^0 have different limiting values when x decreases to 0. But this is a mistake. We must define x^0=1 for all x , if the binomial theorem is to be valid when x=0 , y=0 , and/or x=-y . The theorem is too important to be arbitrarily restricted! By contrast, the function 0^x is quite unimportant.
Published by Addison-Wesley, 2nd printing Dec, 1988.
As a rule of thumb, one can say that 0^0 = 1 , but 0.0^(0.0) is undefined, meaning that when approaching from a different direction there is no clearly predetermined value to assign to 0.0^(0.0) ; but Kahan has argued that 0.0^(0.0) should be 1, because if f(x), g(x) --> 0 as x approaches some limit, and f(x) and g(x) are analytic functions, then f(x)^g(x) --> 1 .
The discussion of 0^0 is very old. Euler argues for 0^0 = 1 since a^0 = 1 for a not equal to 0 . The controversy raged throughout the nineteenth century, but was mainly conducted in the pages of the lesser journals: Grunert's Archiv and Schlomilch's Zeitshrift. Consensus has recently been built around setting the value of 0^0 = 1 .
|
|
|