SOLUTION: x+1=9x^3 + 9x^2 solve the polynomial equation. Been working on this one for awhile and i cant seem to get this one. 4 answers it needs.

No, it only needs 3 "answers", "solutions" or "roots", whichever
label you wish to give them.  That's because the degree (largest
exponent of x) is 3.



Get zero on the right:



Multiply through by -1 so leading coefficient will be
positive:




Possible rational zeros are

±1, ±, and ±

By DesCartes' rule of signs, there is one positive
answer (solution or root), and 2 or 0 negative ones.

Let's try x=1, that is, divide by x-1 to see if
1 is a solution:

1 | 9   9   -1   -1
  |     9  -18  -19
   ----------------
    9 -18  -19  -20

Nope, the remainder is -20, not zero, so x-1 is not a
divisor of 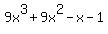, and so x=1 is not
a solution.

Let's try x=-1, that is, divide by x+1 to see if
-1 is a solution:

-1 | 9   9  -1 -1
   |    -9   0  1
   --------------
     9   0  -1  0

Aha! The remainder is zero, so x+1 is a divisor of
of 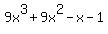, and therefore x=-1 is a
solution.

Anytime we divide by synthetic division and get a zero 
remainder, we have factored the polynomial.  In this
case we have factored 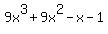 and now
we have



or eliminating the 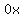 term:



Now we can factor the expression in the second parentheses
as the difference of two perfect squares and get:



Setting each factor = 0,

x+1=0 gives x=-1

3x-1=0 gives x=

3x+1=0 gives x=

Edwin