Question 220640: A physician monitored the effects of aspirin in patients and found that if originally 200mg of aspirin is administered for a headache, sometime later, say 20minutes, only 50% of the aspirin will still be in the bloodstream. after 40 minutes, only 50 mg will still be in the bloodstream and after 60 minutes, only 25mg.
a) determine a formula to establish the amount of aspirin in the bloodstream after t minutes.
b) how long will it take for the bloodstream to be free of aspirin?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! amount of aspirin in the bloodstream is 1/2 of the original amount every 20 minutes.
-----
formula is:
y = 200*(.5)^(.05x)
-----
graph of this equation looks like this:

-----
this equations looks like it models it pretty well.
y is the amount of aspirin left in the bloodstream.
x is the number of minutes.
the horizontal lines are at 200,100,50,25 to show you the amount of aspirin left in the bloodstream after 0,20,40,60 minutes.
-----
It does not appear that the bloodstream will ever be completely free of aspirin based on this formula.
.5^(.05x) will never be equal to 0.
It will become very small, but never zero.
the calculator might show 0, but that's because the calculator can only go so far in the number of decimal places it can show, even with scientific notation.
-----
My calculator shows a result of 0 when 200 is multiplied by .5^333
It shows 2.285974783 * 10^-98 when 200 is multiplied by .5^332
Since .05*x = 333 when the calculator give a result of 0, this means that x = 20*333 = 6660 minutes
That's 4.625 days for the body to be completely free of aspirin enough so that my calculator can't determine how much is still left.
-----
best thing to do with this is determine a point at which the level of aspirin in the blood is less than a certain amount.
-----
that can be calculated.
-----
assume that amount is 1 milligram.
-----
formula would be 1 = 200*(.5)^(.05x)
divide both sides of this formula by 200 to get:
1/200 = (.5)^(.05x)
take the log of both sides of this equation to get:
log(1/200) = (.05x)*log(.5)
divide both sides of this equation by log(.5) to get:
log(1/200)/log(.5) = (.05x)
solve for (.05x) to get:
(.05x = 7.64385619
solve for x to get:
x = 152.8771238 minutes
-----
this means that it will take 152.8771238 minutes for the aspirin in the bloodstream to be less than 1 milligrams.
-----
the following graph should show that about as clear as can get with the tools available.
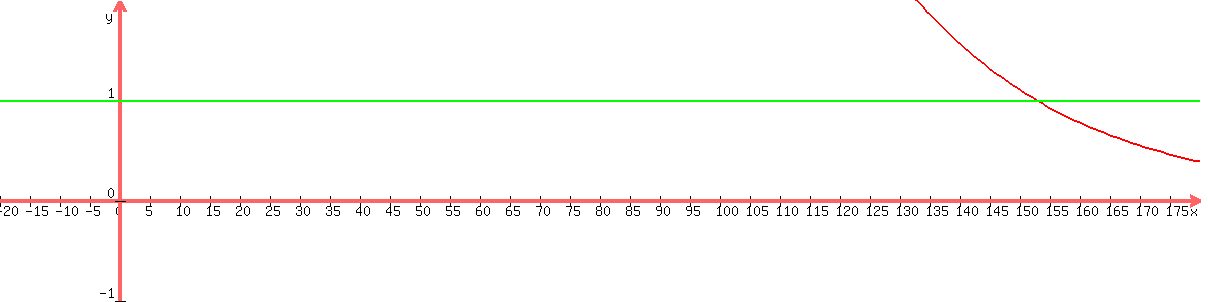
I added the horizontal line at y = 1 to show you the cutoff point better. It's at somewhere around x = 153 which is just about right.
|
|
|