Divide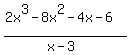 
using synthetic division
Change the sign of the 
in 
to 
Start with this
3 | 2 -8 -4 -6
|
-------------
Bring down the 2
3 | 2 -8 -4 -6
|
-------------
2
Multiply the 2 by the 3, getting 6.
Then write it above and to the right
of the 2:
3 | 2 -8 -4 -6
| 6
-------------
2
Combine the -8 and the 6, getting -2 and
write it at the bottom:
3 | 2 -8 -4 -6
| 6
-------------
2 -2
Multiply the -2 by the 3, getting -6.
Then write it above and to the right
of the -2:
3 | 2 -8 -4 -6
| 6 -6
-------------
2 -2
Combine the -4 and the -6, getting -10 and
write it at the bottom:
3 | 2 -8 -4 -6
| 6 -6
-------------
2 -2 -10
Multiply the -10 by the 3, getting -30.
Then write it above and to the right
of the -10:
3 | 2 -8 -4 -6
| 6 -6 -30
-------------
2 -2 -10
Combine the -6 and the -30, getting -36 and
write it at the bottom:
3 | 2 -8 -4 -6
| 6 -6 -30
-------------
2 -2 -10 -36
Now we interpret that bottom line of numbers:
The largest power of x in the original numerator
is 3. So subtract one from
3 and get 2 for the exponent of x. So the first
three numbers on the bottom is to be interpreted
as
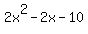Then the last number, -36, is the remainder and
we put that over the original divisor
and this fraction is added to the quotient:
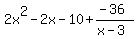Now we can just write that as MINUS that fraction:
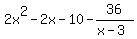Edwin
