Question 203063: (15ab/4)(8/9a^2b^2)= ?
(6a/8b)/(10c/12d)= ?
(2x^2+x-3/9)[(x+1)^2/2x^2+5x+3)= ?
(1/25-y^2)/(6-3y/y^2-7y+10)= ?
Thanks!
Answer by PRMath(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! 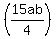 * *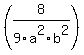
I won't know how to put this in nice fractions for you, so I'll explain, as best as I can, what I'm doing............
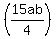 * *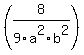
The 15 and the 9 can each be reduced when divided by 3. They become 5 and 3.
The 4 and the 8 can each be reduced when divided by 4. They become 1 and 2
The ab in the numerator can be canceled, but that changes the  and the and the  in the denominator to: in the denominator to: 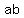
SO when we reduce and cancel, we get:
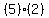 / /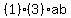 .........OR......... .........OR.........
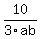
NEXT QUESTION:
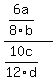
The above is how I am reading your question. If I am correct, then we would do that problem the way we would do any division problem when we work with fractions. In other words, when you divide with a fraction, you MULTIPLY by the reciprocal. So your problem is now........
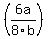 * *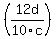
The 6 and the 10 can be reduced when divided by 2. They become 3 and 5.
The 12 and the 8 can be reduced when divided by 4. They become 3 and 2.
Your problem is now............
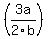 * *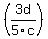 and this is: and this is:
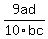
NEXT QUESTION:
 / / * *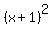 / /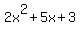
If I have written your problem correctly, then it can be factored like this:
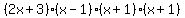 / /
So the (2x + 3) in the numerator can be canceled with the (2x+3) in the denominator.
The (x + 1) in the numerator can be canceled with the (x + 1) in the denominator.
That leaves you with:
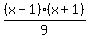
I am sorry to say that your last problem I don't think I'm seeing correctly. Can you repost it, please? It's this part of the problem I'm not sure about:
(1/25-y^2)
I am not sure you have written it correctly. The second part is easily factored. The (6 - 3y) can be factored to 3(2 - y) and the  can be easily factored to (y-5)(y-2). I just am not certain your first part of the problem is written correctly. can be easily factored to (y-5)(y-2). I just am not certain your first part of the problem is written correctly.
I hope this helps .......
|
|
|