Question 202816: 1ST QUESTION:Which of the follow best describes the slope, m=2\3
2nd question:Determine if the lines are parallel, perpendicular, same line, or none of the above. y= -3/5x+2 & 3x+5y=20
3rd:Find the equation for the line through(2,6)y=-5/4x+1 and perpendicular to .
Answer by PRMath(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1ST QUESTION:Which of the follow best describes the slope, m=2\3
You didn't list anything that follows under what best describes a slope of
m = 2/3 so, I'm not sure what you are looking for here. If there was a choice, tho, that said m = 2/3 is the same as saying you rise up 2 and go over 3, from the y-intercept, then that would be the correct slope.
2nd question:Determine if the lines are parallel, perpendicular, same line, or none of the above. y= -3/5x+2 & 3x+5y=20
Here are a couple of facts to help you:
First, parallel lines have the SAME slope
Second, perpendicular lines have slopes that are opposite reciprocal of one another. SO if you had a slope of 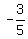 , then a line perpendicular to that would have a slope of: , then a line perpendicular to that would have a slope of:  . .
So in your first line, you have: y = -3/5x + 2. Since the line is in the
y = mx + b format, where "m" is the slope, then in this equation, your slope equals 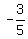 . .
A line PARALLEL to that line would have a slope of 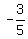
A line PERPENDICULAR to that would have a slope of 
So the second line is this: 3x+5y=20 What is the slope of this line? Well, we don't know until we put it in the y = mx + b format, which means we have to solve for y. So let's do that:
3x+5y=20 (original equation)
5y = -3x + 20 (subtracted 3x from both sides)
y = 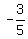 x + x + 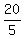 (divided both sides by 5) (divided both sides by 5)
y = 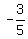 x + 4 (final answer) x + 4 (final answer)
What is the slope of this line? It is 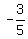 It didn't matter that the y intercept in this equation is 4 and the y intercept in the previous equation was 2. What matters (when speaking about lines being parallel and perpendicular) is the SLOPE. It didn't matter that the y intercept in this equation is 4 and the y intercept in the previous equation was 2. What matters (when speaking about lines being parallel and perpendicular) is the SLOPE.
Ok then, our two slopes are EQUAL and therefore the lines are PARALLEL.
3rd:Find the equation for the line through(2,6)y=-5/4x+1 and perpendicular to .
Unfortunately, you didn't tell me what this line must be perpendicular to, so I cannot solve this question for you. Can you re post please?
I hope this helps.........
:-)
|
|
|