SOLUTION: State the domain of the following and provide a brief explanation of the answer. m(x)=5/x^2-9 l(x)=5x-4 g(x)=7x=4/x=4

Algebra ->  Equations -> SOLUTION: State the domain of the following and provide a brief explanation of the answer. m(x)=5/x^2-9 l(x)=5x-4 g(x)=7x=4/x=4      Log On


   

Question 202423: State the domain of the following and provide a brief explanation of the answer.
m(x)=5/x^2-9
l(x)=5x-4
g(x)=7x=4/x=4
Found 2 solutions by dyakobovitch, jsmallt9:
Answer by dyakobovitch(40) About Me  (Show Source):
You can put this solution on YOUR website!
To find the domain of a function, it is most appropriate to create a graph. Domain satisfies the bounds for the x-axis, or the horizontal movement of the graph.
M(x)=5/x^2 - 9 is a rational function with the following graph: +graph%28+300%2C+200%2C+-20%2C+20%2C+-20%2C+20%2C+5%2Fx%5E2+-+9%29+, so the domain is (-∞,∞).
L(x)=5x-4 is a linear equation with the graph: 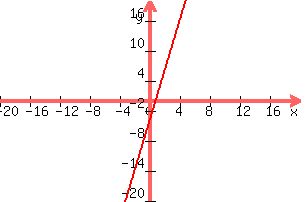+graph%28+300%2C+200%2C+-20%2C+20%2C+-20%2C+20%2C+5x-4%29+. As seen in the graph, it is a line that has no bounds in the Cartesian Coordinate plane.
Its domain is (-∞,∞).
G(x)=7x=4/x=4. If you can clarify the equation I can help you, but this is clearly not a function since there are three equal signs.

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
The domain of a function is the set of all possible values for the input variable, which is usually "x". Generally, when a domain is not explcitly defined, the domain of a function is all Real numbers. However, one must exclude values which cause expressions which cannot be allowed.

Examples of expressions which cannot be allowed:
  • Division by zero
  • Negative radicands of even-numbered roots:
    • g%28x%29+=+sqrt%28x+%2B+3%29 Since there are no square roots of negative numbers (within the set of Real numbers) the domain of g must ensure that (x+3) >= 0. In other "words", x >= -3.
    • h%28x%29+=+root%286%2C+3x+-+6%29. Since there are no 6th roots of negative numbers (within the set of Real numbers) the domain of h must ensure that (3x - 6) >= 0. In other "words", x >= 2.
    • Note that q%28x%29+=+root%283%2C+4x+%2B+9%29 has a domain of all real numbers since cube roots (in fact all odd-numbered roots) of negative numbers do exist within the set of Real numbers.
  • Negative or zero agruments to logarithm functions (regardless of the base of the logarithm).
  • Arguments which are not allowed by certain other functions which are part of the definition of the function in question. An example of this would be f(x) = tan(x) + 4. Since the tan function is not defined for 90 degrees (or pi%2F2 radians), these values must be excluded from the domain of f(x).

Now let's apply this to your problems.

m%28x%29=5%2F%28x%5E2-9%29
Since we have a denominator we must avoid x-values that would make the denominator zero. So if we solve x%5E2+-+9+=+0 we will find the x-values we must exclude from the domain. Factoring this equation we get %28x+%2B+3%29%28x+-+3%29+=+0. From this we can see that the solution is x = 3 or x = -3.
So the domain of m(x) is all real numbers except 3 and -3.

l(x)=5x-4
Since none of the items described above (denominators, even-numbered roots, logarithms, etc.) are present, there is nothing to exclude. The domain is all Real numbers.

g(x)=7x=4/x=4
With 3 equal signs I'm not sure what this is. Since the "=" and the "+" are on the same key, I'm going to assume that the last two "=" are supposed to be "+".
If g%28x%29+=+7x+%2B+4%2Fx+%2B+4 we must make sure the denominator of x does not become zero. So we must exclude 0 from the domain.
If instead g%28x%29+=+7x+%2B+4%2F%28x%2B4%29 then we must make sure (x + 4) is not zero. So x must not be -4.