Question 201386: Solve the inequality
p^3-16p(< or =)0
possible answers
(-infinite,-4] or (0,4)
(-infinite,-4] or (0,4]
(-infinite,-4) or (0,4)
(-infinite,-4) or (0,4]
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I think I started this one yesterday, clicked on "post answer" accidentally and then couldn't find the problem again to finish my response. Let's try it again.
First factor the left side. Start, as always, by factoring out the Greastest Common Factor (GCF) which in this case is p:
Now factor 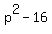 as a difference of squares
By factoring the inequality we now know that the product of three numbers is less than zero. In other words the product is negative. If we think about multiplying three numbers and getting a negative result we should be able to tell that one of the following must be true- All three numbers are negative.
- Two numbers are positive and one number is negative.
If we think about the three factors we should also be able to tell which factor is the largest, which is the smallest and which is "in between" the other two even though we have no idea what numbers they are! We should be able to tell, no matter what number "p" is, that:- (p+4) must be the largest
- (p-4) must be the smallest
- (p) must be the "in between" factor
Try to make sense out of the above so you can possibly figure out similar problems on your own in the future.
Now that we know the order of the factors and the possibilities for the factors we are in a position to get some answers. First we will consider the case of "All three factors are negative". Think about larger and smaller numbers on the number line. Smaller is always to the left of the larger, right? So if the largest factor is negative (left of zero on the number line), won't the two smaller factors (which are left of the largest) have to be negative also? (Again, try to make sense of this.)
So if the largest factor is negative then all three factors will be negative. In other "words" if  all three factors will be negative. Solving this in equality by subtracting 4 from both sides we get
The second case is when two factors are positive and one is negative. Using logic like the logic we used on the first case we can determine that this combination of factors can only occur when the smallest factor is negative and the other two are positive. And the other two will be positive if the "in between" factor is positive. This can be expressed with the following inequalities:
 and 
By adding 4 to both sides of the first inequality we get
 and Our complete solution, including both cases, is
 or ( and )
In interval notation this is:
(-infinity,-4] or [0,4]
NOTE 1: This is NOT one of the answers you provided! The brackets, "[" aand "]", mean that the endpoint is included in the solution and parentheses mean up to bu not including the endpoint. The three brackets in "(-infinity,-4] or [0,4]" are all correct because -4, 0 and 4 are all solutions to this inequality! Every possible answer you provided has a parenthesis next to one or more of these numbers and therefore the provided answers all leave out one or more numbers which should be included. NOTE 2: The logic above addressed the solutions for a product that was negative. By including the "or equal to" in each of our inequalities we addressed the possibility that the product could be zero instead.
|
|
|
