I assuming that the actual problem is 
. If this is incorrect, disregard the rest.
To solve . factor the left side:
Factor out the GCF which is p:
Then factor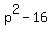 
as a difference of squares giving:
Even though we do not know what number "p" may be we should be able to determine that- (p+4) must be the largest of the three factors
- (p-4) is the smallest of the three factors
- p must be the "in between" factor.
Now we have a product of three numbers which is negative (or zero). If you think about it you can figure out that that there are only two ways this could happen:- All three numbers are negative
- Two numbers are positive and one is negative.
We will get solutions from both possibilities.
1. All three numbers are negative. The easiest way to make all three numbers negative is to make the largest number negative. (Think about a number line. Larger numbers are to the right and smaller numbers are to the left. If (p+4) is negative (left of 0) and if p and (p-4) are to the left of (p+4), won't p and (p-4) also be the the left of 0 (negative)?) So:
will make all three numbers negative. Subtracting 4 from both sides we get
This is part 1 of our solution.
2. Two numbers are positive and one is number is negative. This can only happen if the smallest number is negative and the other two are positive. (Think about it.) Using logic like the earlier solution we can make the two larger numbers positive by making the "in between" number positive. So to get one negative factor and two positive factors if both of the following are true:
Adding 4 to both sides of the first inequality we get
This is the second part of the solution.
The complete solution is:
[[[p < -4 or (p <= 4 and p >= 0)}}}
In words, "p" must be a number less than -4 OR "p" must be a number between 0 and 4 (inclusive).
(