Question 183211: "find all integers m for which y^2+my+50 can be factored?"
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, multiply the first coefficient 1 and the last term 50 to get 50. Now list the factors of 50
Factors of 50:
1,2,5,10,25,50
-1,-2,-5,-10,-25,-50
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*50
2*25
5*10
(-1)*(-50)
(-2)*(-25)
(-5)*(-10)
Now add up each paired factor (ie 1+50=51, 2+25=27, etc..):
| First Number | Second Number | Sum | | 1 | 50 | 1+50=51 | | 2 | 25 | 2+25=27 | | 5 | 10 | 5+10=15 | | -1 | -50 | -1+(-50)=-51 | | -2 | -25 | -2+(-25)=-27 | | -5 | -10 | -5+(-10)=-15 |
All of the numbers in the last column are possible values for the value of "m". Remember, you can only factor  only if the factors of only if the factors of 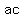 add to "b" add to "b"
So the possible values for "m" are: 51, 27, 15, -51, -27, -15
Note: all of these values of "m" are straight from that third column.
This means that the following quadratics are factorable:
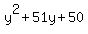 , ,
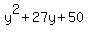 , ,
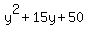 , ,
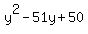 , ,
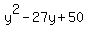 , and , and
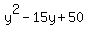
|
|
|