Question 173454: Not sure if this is the appropiate topic but.
A motorboat travels 325km in 5 hours going upstream and 534 km in 6 hours going downstream. What is the speed of the boat in still water and what is the speed of the current? I don't understand this. How can still water have a speed? I am totally lost. Van you help me figure this out? Thanks, Judy
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! A motorboat travels 325km in 5 hours going upstream and 534 km in 6 hours going downstream. What is the speed of the boat in still water and what is the speed of the current?
--------
It is not still water; it is moving water, or current.
--------
Upstream DATA:
distance = 325 km ; time = 5 hrs; rate = d/t = 325/5 = 65 km/h
------------------
Downstream DATA;
distance = 534 km ; time = 6 hrs ; rate = d/t = 534/6 = 267/3 = 89 km/h
-----------------------------------
EQUATIONS:
b + c = 89
b - c = 65
---------------
Add to solve for b: (b is the speed of the boat in still water)
2b = 154
b = 77 km/h (speed of the boat in still water)
------------
If b+c = 89 then c = 12 km/h (speed of the current)
======================================================
Cheers,
Stan H.
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! Still water doesn't have any speed. That's the point. Saying the speed of the boat in still water is the same as saying the speed of the boat if there were no current. Since the current in a river flows in the downstream direction (by definition of downstream), when the boat is going downstream its speed relative to the bank of the river is the speed in still water plus the speed of the current. Conversely, going upstream, the speed of the current is subtracted from the speed of the boat in still water to get the speed relative to an observer on the bank of the river.
So:
Start with the basic formula that relates distance, rate (or speed), and time:
 which can also be expressed as 
Let's say that the relative speed for the upstream trip is 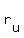 , since we know that an upstream trip of 325 km takes 5 hours, we can say that  km/hr.
Likewise, the downstream trip is given by  km/hr.
Now, let's say the speed of the boat in still water is  and the speed of the current is 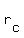 . Since the current subtracts from the boat speed going upstream and adds going downstream, we can write the following two equations:
Here we have a system of two linear equations in two variables. Since the coefficients on the 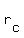terms are additive inverses, just add the two equations, term by term:
 km/hr.
So the speed of the boat in still water is 77 km/hr.
Since we know that , we can substitute:
 km/hr
Meaning the speed of the current is 12 km/hr.
|
|
|
