system of equation with four variables.
x + y + z + w = 0
x + y - z - w = 1
x - y + z + w = 3
x - y - z + w = -1
We can eliminate y, z and w simply
by adding the second and third equations,
term by term
x + y - z - w = 1
x - y + z + w = 3
-------------------
2x = 4
2x = 4
x = 2
Substitute 2 for x in the
original equations.
2 + y + z + w = 0
2 + y - z - w = 1
2 - y + z + w = 3
2 - y - z + w = -1
y + z + w = -2
y - z - w = -1
-y + z + w = 1
-y - z + w = -3
The third equation is just the
second equation multiplied by
-1, so we can eliminate it:
y + z + w = -2
y - z - w = -1
-y - z + w = -3
We can eliminate both z and w
by adding the first and second
equation:
y + z + w = -2
y - z - w = -1
---------------
2y = -3
2y = -3
y = 
Substitute for y
in the three:
+ z + w = -2
- z - w = -1
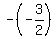- z + w = -3
+ z + w = -2
- z - w = -1
- z + w = -3
Multiply each through by 2 to
eliminate the fractions:
-3 + 2z + 2w = -4
-3 - 2z - 2w = -2
3 - 2z + 2w = -6
2z + 2w = -1
-2z - 2w = 1
-2z + 2w = -9
The second equation is just the
first equation multiplied by -1,
so we can eliminate it:
2z + 2w = -1
-2z + 2w = -9
Now we can eliminate z by adding
those two equations:
2z + 2w = -1
-2z + 2w = -9
---------------
4w = -10
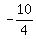w = 
w = 
So (x,y,z,w) = (2,,2,)
Edwin
