SOLUTION: Where are you looking if the indices i and j are equal in a square matrix? a. Along the middle row b. Along the middle column c. Along the diagonal from the upper left to the lo

Notice in the matrix:



the way the elements have subscripts, for instance,
 means the element where  
and .

The first subscript, which is denoted by , is
the number of the row it's in and the second subscript,
which is denoted by  is the number of the column 
that it's in.



So picking out the elements where i and j are equal,
they are 
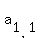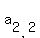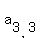, , , and    

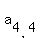Notice they appear on the diagonal that goes from the upper
left corner to the bottom right corner.

So the answer is (c).

Edwin