Question 146271:
Please find the domain of H(x)=√(25-x₂)
Thank You
Found 2 solutions by Fombitz, Edwin McCravy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please find the domain of 
Thank You
Note that  means the same as means the same as 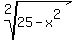 ,
with the index ,
with the index  understood.
If a radical has an even index, that is: understood.
If a radical has an even index, that is:
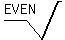 , such as , such as  , ,  , , 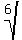 , etc.
then what is under the radical must not be negative.
Non-negative means "positive or 0", and "positive" means "greater that 0",
therefore what is under the radical must be greater than or equal to 0.
So we make an inequality that says , etc.
then what is under the radical must not be negative.
Non-negative means "positive or 0", and "positive" means "greater that 0",
therefore what is under the radical must be greater than or equal to 0.
So we make an inequality that says  is greater than or equal to 0. is greater than or equal to 0.
 We find all critical values by setting the left side = 0:
We find all critical values by setting the left side = 0:


 , , So we draw a number line and mark those numbers
<----------o-----------------------------o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number left of -5, say -6.
Substitute it in the original inequality:
So we draw a number line and mark those numbers
<----------o-----------------------------o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number left of -5, say -6.
Substitute it in the original inequality:



 This is false so we do not shade to the left of -5.
We still have this number line.
<----------o-----------------------------o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number right of -5 but left of 5, say 0.
Substitute it in the original inequality:
This is false so we do not shade to the left of -5.
We still have this number line.
<----------o-----------------------------o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number right of -5 but left of 5, say 0.
Substitute it in the original inequality:



 This is true so we do shade to the line between -5 and +5,
like this:
<----------o=============================o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number right of 5, say 6.
Substitute it in the original inequality:
This is true so we do shade to the line between -5 and +5,
like this:
<----------o=============================o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Next we choose a number right of 5, say 6.
Substitute it in the original inequality:



 This is false so we do not shade to the right of 5.
Next we must test the critical values in the original inequality
Testing
This is false so we do not shade to the right of 5.
Next we must test the critical values in the original inequality
Testing 



 This is true so we darken the circle at -5.
<----------@=============================o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Testing
This is true so we darken the circle at -5.
<----------@=============================o--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Testing 



 This is also true so we also darken the circle at 5.
<----------@=============================@--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
The interval notation for that is the abbreviation
for the above number line graph:
[-5,-5]
Edwin
This is also true so we also darken the circle at 5.
<----------@=============================@--------->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
The interval notation for that is the abbreviation
for the above number line graph:
[-5,-5]
Edwin
|
|
|