SOLUTION: Which of the following is another version of {{{f(x) = 2x^2 - 4x - 7}}} ? a. {{{f(x) = 2(x -1)^2 - 9}}} b. {{{f(x) = (x - 1)^2 - 9}}} c. {{{f(x) = (x + 1)^2 - 1/2}}} d. {{{f(x

We can eliminate d because none of the choices are
factorizations of f(x) anyway.

The easy way to find which one is correct is to substitute
an arbitrary value for , ( is a good choice since it's easy)
in the original and in each of the choices.

Substituting x=0 in the original:





Now substitute  in the answer a.



 




So a. is possible.

Now substitute  in the answer b.



 




So b. is NOT possible.

Now substitute  in the choice c.




 





So c. is NOT possible.

Thus the only possible choice is a.

--------------

However, that's not what your teacher wants you
to do, although it is one way to get the correct
answer on a multiple choice test. I just thought 
I'd show you the above method of substituting in
each of the answers to rule out the incorrect 
choices. This may save you from having to miss a 
problem which you can't solve on a multiple 
choice test. Of course, this method will not work 
on the kind of test where you have to show your 
work.

-------------

Here is what your teacher wanted you to do:



Factor 2 out of the first two terms only:



We will complete the square inside the parentheses:

Multiply the coefficient of x, which is -2, by ,
getting -1.  Then square -1 getting +1

So add +1 and immediately subtract 1 inside the 
parentheses:



Change the parentheses to brackets so they can hold 
parentheses:

[]

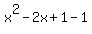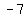Factor only the first three terms inside the brackets:

[]

[]

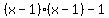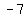
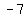Now remove the brackets by distributing the 2, leaving
the 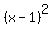 intact:



Combine the  and the  and get 



which is choice a.

Edwin