Question 131519: a=b+2
a+b=axb
show that a and b are not integars
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm assuming that your 'axb' really means 'a times b'
So:
 and and 
Substitute into the second equation:


Add -2b to both sides:

So:  or or  , therefore , therefore  or or 
1. Assume that  is a rational number, meaning that there exists an integer is a rational number, meaning that there exists an integer  and an integer and an integer  such that such that  . .
2. Then  can be written as an irreducible fraction can be written as an irreducible fraction 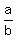 such that such that  and and  are coprime integers and are coprime integers and  . .
3. It follows that  and and  . ( . ( ) )
4. Therefore  is even because it is equal to is even because it is equal to 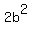 . . 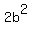 is necessarily even because it's divisible by 2—that is, is necessarily even because it's divisible by 2—that is,  — and numbers divisible by two are even by definition.) — and numbers divisible by two are even by definition.)
5. It follows that  must be even as (squares of odd integers are also odd, referring to b) or (only even numbers have even squares, referring to a). must be even as (squares of odd integers are also odd, referring to b) or (only even numbers have even squares, referring to a).
6. Because  is even, there exists an integer k that fulfills: is even, there exists an integer k that fulfills:  . .
7. Substituting 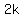 from (6) for from (6) for  in the second equation of (3): in the second equation of (3):  is equivalent to is equivalent to  is equivalent to is equivalent to  . .
8. Because  is divisible by two and therefore even, and because is divisible by two and therefore even, and because  , it follows that , it follows that  is also even which means that b is even. is also even which means that b is even.
9. By (5) and (8) a and b are both even, which contradicts that a / b is irreducible as stated in (2).
Since there is a contradiction, the assumption (1) that  is a rational number must be false. The opposite is proven: is a rational number must be false. The opposite is proven:  is irrational. (courtesy Wikipedia) is irrational. (courtesy Wikipedia)
Since all integers can be represented as the quotient of integers, all integers are rational. Since  has been proven to be irrational, has been proven to be irrational,  cannot be an integer. Since all integers can be represented as the sum of 2 and some other integer and cannot be an integer. Since all integers can be represented as the sum of 2 and some other integer and  has been shown to be other than an integer, has been shown to be other than an integer, 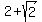 and and 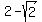 are also not integers. are also not integers.
|
|
|