Question 125480: Hi. Can I have some help finding the domain of this function?
g(x)=√x/2x^2+x-1
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think you meant the function to be  rather than rather than 
The domain of a function is the set of all real values that x can take on such that the function is defined. I'm also presuming that you are mapping the function to 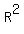 . .
Since  is undefined if is undefined if  , and , and 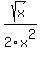 is undefined at zero, the domain range is ( is undefined at zero, the domain range is ( , , ) )
If, on the other hand you really meant the alternative function above with the entire expression under the radical, you could immediately say that zero is excluded from the domain, but you would have to work out the value for x that would cause 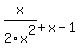 to be less than zero. to be less than zero.
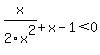
Multiply by 
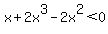
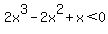
Now, if we make a graph of  , we should be able to see where the function is less than zero, at least in an approximate sense. , we should be able to see where the function is less than zero, at least in an approximate sense.
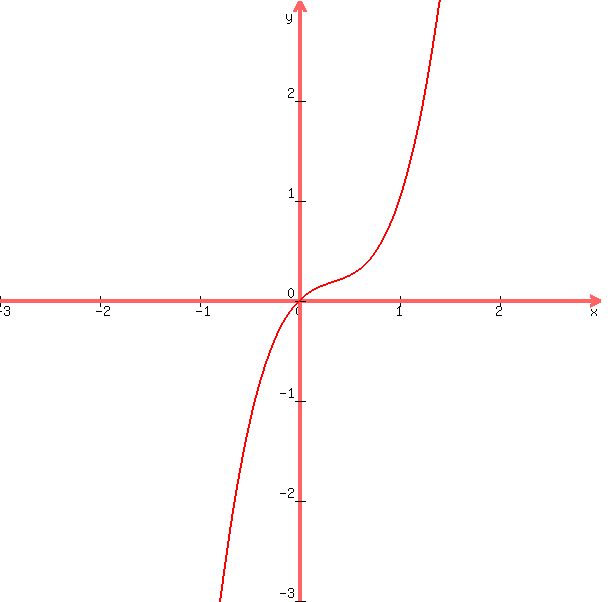
Looking at this graph, we see that the only real number zero of the function is at zero, so the interval for which  is where is where  . .
That means that the domain of  is the same regardless of whether is the same regardless of whether  or or  , namely: ( , namely: ( , , ) )
The following graphs are of both original functions. The green one is the first way, and the red one is the one with the entire expression under the radical. You can see that the graph visually supports the analysis of the domain interval.

|
|
|