Question 12201: Can you please help to answer the following question:
.
Find all positive integers a and b such that:
a^2+b^2-7=ab
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! At first,note that a^2+b^2-7=ab -->a^2+b^2 = ab +7.
So, if a,b are positive then a^2+b^2 > 7.
Convert a^2+b^2-7=ab to  i.e. i.e.
 . Hence, . Hence, 
Also, notice a & b are symmetric.
[note a,b are positive integers with 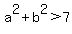 and and  ] ]
Consider the table below (using Excel or direct computation)
a b a^2+b^2-ab
1 3 7
1 4 13
1 5 21
1 6 31
1 7 43
2 2 4
2 3 7 [No need to check a >= 3, why ?]
The only pairs (a,b) with  satisfying a^2+b^2-ab = 7 are satisfying a^2+b^2-ab = 7 are
(1,3) and (2,3). Hence,we also have (3,1) and (3,2)
So,there are 4 pairs of positive integer solutions:
(1,3),(2,3), (3,1) and (3,2)
Kenny
|
|
|