SOLUTION: 8^x=16^x+4

I read this equation exactly and literally as it is written

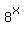     =  + .     (1)



My statement is that this equation has no solutions in real numbers.



Indeed, if  x >= 0,  then, obviously, 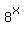   is less than  ;

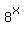Hence, a fortiori,   <  + ,  so equation (1) has no solutions in the domain  x >= 0.



Next, if  x < 0,  then left side of equation (1) is less than 1,
while right side of this equation is greater than 4, so equation (1) has no solutions in the domain   x < 0.



Thus the statement is proved and the equation has no solutions in real domain.

If, in opposite, your original equation is

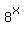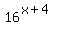     = ,    (2)


then the reasoning is different and the answer is different, too.


Then this equation (2) can be rewritten equivalently in base '2'

     = ,


which implies an equation for indexes

    3x = 4*(x+4),

    3x = 4x + 16,

    3x - 4x = 16,

       -x   = 16,

        x   = -16,


so the solution for equation (2) is x = -16.