Question 1208849: Find the real solutions of the given equation. Use a calculator to express solutions rounded to two decimal places.

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Make the "change of variable"  and turn the equation into the quadratic equation and turn the equation into the quadratic equation

Then you could use the quadratic formula that says that the solutions to
 are given by are given by 
For the equation above  , ,  , and , and 
You get  (rounded), and (rounded), and
 (rounded) (rounded)
At this point, if as I suspect you were not taught about complex and imaginary numbers, you can only list real solutions.
Then,  has no real solutions, and your solutions would be has no real solutions, and your solutions would be
 and and 
NOTE:
If you are not fond of the quadratic formula, "completing the square" would be an option,
if you were taught to transform something like 
into  , add , add 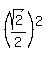 to both sides to both sides
to get  , ,
rewrite it as  and and  for the solutions for the solutions
 and and 
They really quote that formula as  for for  , ,
but the name/letter used for the variable makes no difference.
|
|
|