SOLUTION: factorise x^4 + 4^2023

Let' start writing

    =  =  =  = .


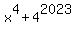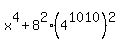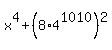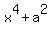It has the form ,  where  a = .



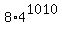Now we will factor  the binomial 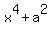   by some tricky way


       =  =  -  = 
    

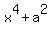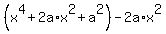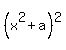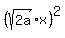    = factorize as the difference of squares =  = .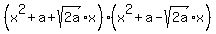


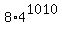Now substitute  a =   into this formula.  Notice that   =  =  =  = .  
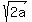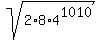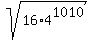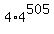You will get


     = ,


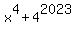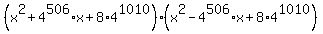or, which is the same,


     = .


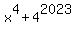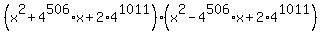It is the desired factorization.