.
You start from
 +
+ 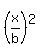 = c.
As your starting equation is written in this form,
it is assumed implicitly that a =/=0, b =/= 0.
Isolate the term with b in the left side
= c.
As your starting equation is written in this form,
it is assumed implicitly that a =/=0, b =/= 0.
Isolate the term with b in the left side
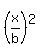 = c -
= c - 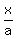 .
Since left side is the fraction, write right side as a fraction, too
.
Since left side is the fraction, write right side as a fraction, too
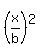 =
= 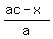 .
It is the same as
.
It is the same as
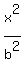 =
= 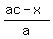 .
Since
.
Since  is now in the denominator, turn both fractions upside down
is now in the denominator, turn both fractions upside down
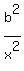 =
=  .
Multiply both sides by
.
Multiply both sides by 
 =
= 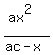 .
Now take square roots of both sides
b = +/-
.
Now take square roots of both sides
b = +/- 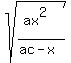 = +/-
= +/- 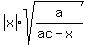 .
Any of these two final expressions is the desired expression for b.
This final expression is valid under assumption that ac-x =/= 0 and the expression under the square root is positive.
.
Any of these two final expressions is the desired expression for b.
This final expression is valid under assumption that ac-x =/= 0 and the expression under the square root is positive.
Solved.