Question 1208085: Determine if each function is even, odd or neither.
A. F(x) = (x)^(1/3) + |x|^2
B. G(x) = (1/x) - (x)^(1/4)
C. H(x) = [(x)^(1/2) + 12x]/(x^3 - 9)
D. S(x) = (x^4 + |x - 4|)/(x^4 - 2x)
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine if each function is even, odd or neither.
A. F(x) = (x)^(1/3) + |x|^2
B. G(x) = (1/x) - (x)^(1/4)
C. H(x) = [(x)^(1/2) + 12x]/(x^3 - 9)
D. S(x) = (x^4 + |x - 4|)/(x^4 - 2x)
~~~~~~~~~~~~~~~~~~~~~~
I will answer (B), (C) and (D).
(B) In (B), (x)^(1/4) is defined only for x >= 0.
Therefore, function G(x) is defined only for x >= 0.
Therefore, the conception of even and/or odd function is inapplicable for G(x).
Therefore, the answer for (B) is "neither".
(C) In (C), (x)^(1/2) is defined only for x >= 0.
Therefore, function H(x) is defined only for x >= 0.
Therefore, the conception of even and/or odd function is inapplicable for H(x).
Therefore, the answer for (C) is "neither".
(D) In (D), calculate S(x) at two values of x: x= 1 and x= -1.
At x= 1, S(1) = 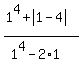 = =  = =  = -4.
At x= -1, S(-1) = = -4.
At x= -1, S(-1) = 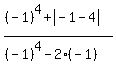 = = 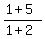 = = 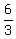 = 2.
So, neither S(1) = S(-1) nor S(1) = -S(-1). Thus we conclude that function S(x) is neither even nor odd. = 2.
So, neither S(1) = S(-1) nor S(1) = -S(-1). Thus we conclude that function S(x) is neither even nor odd.
Parts (B), (C) and (D) are solved and answered, with explanations.
|
|
|